Прежде чем перейти к рассмотрению вопроса о роли симметрии в композиции орнамента, условимся о более широком содержании понятия «симметрия».
Простейшим видом симметрии является отражение в зеркале какой — либо фигуры. Поэтому говорят, что фигура обладает зеркальной симметрией, если она может быть разделена прямой линией на две равные части, расположение которых подобно отражению в зеркале.
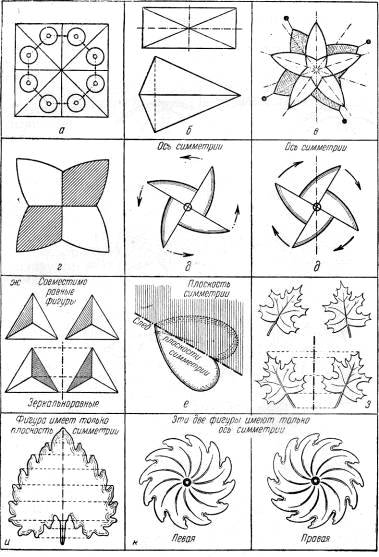
Примером зеркальной симметрии может служить деление квадрата на две равные части его диагональю (рис. 37, а). Но диагональ прямоугольника, хотя и разделит его на две равные части, однако расположение этих частей не обладает признаком зеркальной симметрии — расположением точек (вершин углов) попарно на одном перпендикуляре к прямой линии — следу плоскости симметрии (т. е. зеркала).
Можно из таких половинок прямоугольника составить симметричную фигуру, но это уже не прямоугольник (рис. 37, б). Известно, что в прямоугольнике можно провести две плоскости симметрии, параллельные парам параллельных сторон прямоугольника. В квадрате таких плоскостей будет четыре. Вещь построена геометрически закономерно или правильно, если ее можно пространственно разделить без остатка на равные части относительно некоторого геометрического признака. Например, квадрат можно разделить на восемь равных прямоугольных треугольников (рис. 37, а). Поэтому симметричным предметом называют такой предмет, который состоит из геометрически и физически равных частей, должным образом расположенных относительно друг друга.
В природе нет предметов идеально симметричных. Существуют следующие отклонения от совершенной симметрии: а) соединение в одной фигуре противоречивых симметрий (рис. 37, в), например, в результате сочетания пятиконечной звезды с четырехконечной в центре первой. Такая фигура в целом асимметрична, но отдельные ее части — обе звезды — симметричны; б) смешение геометрического и физического равенства частей симметричной фигуры, изображенной на рис. 37, г. Путем окраски двух из четырех равных частей этой фигуры можно получить только двойную симметрию с физической точки зрения, тогда как с геометрической точки зрения фигура может быть разложена на четыре равные части; в) обычно симметричными называют только такие фигуры, в которых есть плоскость симметрии (рис. 37, е, и). В новом виде симметрии, о котором сейчас будет идти речь, плоскостей симметрии нет, но есть ось симметрии — линия, при полном обороте вокруг которой фигура несколько раз приходит в совмещение сама с собой (рис. 37, д, к). Ось симметрии проходит через центр фигуры перпендикулярно к плоскости рисунка. На рис. 37, ж изображены фигуры совместимо равные и зеркально равные.
37. Примеры симметрии.
Если построить на основе зеркальной симметрии две одинаковые фигуры, имеющие лишь ось симметрии, то окажется, что эти фигуры относятся друг к другу, как правая рука к левой, поэтому целесообразно назвать одну из них правой, а другую левой. Обе эти фигуры геометрически равны друг другу (рис. 37, к). Для краткости условимся обозначать плоскость симметрии буквой М, а ось симметрии буквой Н.
Симметрия является одним из важных признаков красоты форм. Проверим это хотя бы на таком примере: возьмем две неправильные, асимметричные, но одинаковые фигуры; порознь взятые они некрасивы, но если мы расположим их на основе зеркальной симметрии, такое их сочетание уже производит более приятное впечатление. Это достигнуто правильностью взаимного расположения частей новой фигуры — ее симметрией (рис. 37, з).